Optimizing Fanduel in R

I want to give a little background on my experience with fantasy football first. If you’re just looking for the algorithm just skip down to the section titled The Algorithm.

Fantasy Football

I like Chicago Bears football. Even during rough seasons like this one. I don’t really care that much about other football teams. So when my friends first invited me to play fantasy football back in 2006, I bought a $5 magazine with rankings of every player. I didn’t do well that year. So the next year I decided to create a drafting algorithm. At the time I was just getting started in R, so I wrote it in Excel. I won the championship that year.

I quit playing for a few years when grad school was intense and recently un-quit. I rewrote the majority of the program in R last year and completed the transition this year. I’ve won my division both years! I’ve been tempted to make it into an app, but there’s already a ton of them. One day I’ll get the time…

Fanduel

Daily fantasy sports (DFS) became huge this year. It got so big that it’s caught the notice of the attorneys general of states like Washington and New York, where they are looking for losers to get their money back. Illinois has now jumped on the anti-DFS bandwagon.

A few months ago I looked into Fanduel and confirmed what I thought to be true… it’s an optimization problem of the kind that I studied in my operations research (OR) classes, different from a season draft in a few important ways. So I put $200 into an account, downloaded the player data from Fanduel and other sources, wrote a program to munge the data, and then applied a good ol' linear programming optimization to it.

With some conditions, linear programming is useful whenever you have limited resources ($60k for player salaries) and a linear combination of values that you want to maximize (fantasy points) or minimize. It was made to help us defeat the Nazi’s, literally.

Linear programming arose as a mathematical model developed during World War II to plan expenditures and returns in order to reduce costs to the army and increase losses to the enemy. It was kept secret until 1947. Postwar, many industries found its use in their daily planning.

I compared my results to those other online algorithms and they were close, but not exact. This told me that I was doing it right and that it was worthwhile to do it myself. After 2 weeks I won 3 of the 6 contests I’d entered and was up to almost $300 in my account. I had dreams of quitting my day job. Then I proceeded to lose every contest I entered until I had lost it all. It turns out that player scoring is highly variable in fantasy football.

Given the Illinois Attorney General’s stance on DFS and the NFL playoffs upon us, I figured I should post this before the teachable moment of linear programming passes. It’s a rare opportunity to have an algorithm so perfectly suited to 15-minutes of pop culture fame.

The Algorithm

This algorithm optimally allocates your $60k fantasy budget so that you get the most points without going over budget. If you knew in advance how many points each player would score, this algorithm would guarantee you have the best team. Of course, you don’t know that.

I’m going to use the kind of data you’d get from a DFS site and just use the average player points per game as their expected scores. I’ll leave out fancier models that modify expected player scores utilizing integration with outside data. I previously used a fancier model and it didn’t win me any money. That doesn’t mean you won’t get it to work! I mean, it probably won’t, but web scraping in R is a topic for another post!

The data is straight-forward; rows for each player, columns for player name, position, expected points, and salary. First we read the data in and order it by position (for clarity below).

dat <- read.csv("DFS.csv")
fd <- dat[order(dat[, "Position"]), ]

It looks like this:

library('knitr')
kable(head(fd), format = "markdown", row.names = F)

install.packages('dummies')

library(dummies)

## dummies-1.5.6 provided by Decision Patterns

Position.Mat <- dummy(fd[, "Position"])
colnames(Position.Mat) <- levels(fd[, "Position"])

Additionally, we’ll need a column for the flex position. Actually, we don’t need this. I originally wrote out the program thinking I’d need it, but for FanDuel, you don’t. You’ll notice this is now handled in the constraints section. If you are a RB, WR, or TE you are an eligible flex player.

Position.Mat <- cbind(Position.Mat, Flex = rowSums(Position.Mat[, c("RB", "TE", "WR")]))

Now that we have the data munged, I’ll be using the lpSolve package to select the optimal players. If you look at the bottom of the help you’ll this:

install.packages("lpSolve")
library(lpSolve)
?lp
# Set up problem:
# maximize
#   x1 + 9 x2 +   x3
# subject to
#   x1 + 2 x2 + 3 x3  <= 9
# 3 x1 + 2 x2 + 2 x3 <= 15

For DFS each variable or dimension is a binary variable (a 1 or 0) representing the selection of a player; e.g. if x1 == 1, then we will be drafting the Seattle Seahawks. Else, x1 == 0 and we will not be drafting the Seattle Seahawks.

Connecting this to the example in the help file, the function we want to maximize is expected points; i.e x1 * 10.8 + x2 * 10.2 + ..., where 10.8 is the expected number of points from the Seahawks and 10.2 is the expected number of points from the Chiefs. If we pick the Seahawks, then x1 == 1 and we would expect 1 * 10.8 + 0 * 10.2 + ... This is called the objective function.

f.obj <- fd[, "Points"]

The component-wise multiplication by xi is implicit in this syntactic formulation.

Next we need to set up the constraints; i.e. the “subject to” part of the help file. Getting our constraints into the format above is easy. We take our salary data, bind it to the position matrix, and transpose it.

f.con <- t(cbind(Salary = fd[, "Salary"], Position.Mat))
colnames(f.con) <- fd$Name
kable(f.con, format = "markdown", row.names = T)

Seattle Seahawks Kansas City Chiefs Houston Texans Pittsburgh Steelers Minnesota Vikings Green Bay Packers Cincinnati Bengals Washington Redskins Steven Hauschka Chris Boswell Mike Nugent Cairo Santos Blair Walsh Dustin Hopkins Nick Novak Mason Crosby Russell Wilson Ben Roethlisberger Aaron Rodgers Kirk Cousins Andy Dalton Alex Smith Brian Hoyer Teddy Bridgewater AJ McCarron Brandon Weeden Landry Jones Chase Daniel Tarvaris Jackson Shaun Hill Robert Griffin III Keith Wenning Colt McCoy Scott Tolzien Adrian Peterson DeAngelo Williams Marshawn Lynch Jeremy Hill Christine Michael Charcandrick West Eddie Lacy James Starks Fitzgerald Toussaint Jordan Todman Alfred Blue Giovani Bernard Jerick McKinnon Alfred Morris Matt Jones Spencer Ware Matt Asiata Bryce Brown Fred Jackson Akeem Hunt Chris Thompson Chris Polk Derrick Coleman Knile Davis Darrel Young Isaiah Pead John Crockett Pierre Thomas Dri Archer John Kuhn Rex Burkhead Jonathan Grimes Jordan Reed Tyler Eifert Travis Kelce Heath Miller Richard Rodgers Kyle Rudolph Luke Willson Ryan Griffin Tyler Kroft Justin Perillo C.J. Fiedorowicz MyCole Pruitt C.J. Uzomah Garrett Graham Demetrius Harris Chase Coffman Cooper Helfet Brian Parker Kennard Backman Jesse James Rhett Ellison Antonio Brown DeAndre Hopkins A.J. Green Doug Baldwin Jeremy Maclin DeSean Jackson Martavis Bryant Randall Cobb Pierre Garcon Tyler Lockett Jermaine Kearse Markus Wheaton Stefon Diggs James Jones Marvin Jones Davante Adams Nate Washington Cecil Shorts Mohamed Sanu Jaelen Strong Albert Wilson Brandon Tate Chris Conley Mike Wallace Jamison Crowder Jeff Janis Jared Abbrederis Rashad Ross Cordarrelle Patterson Charles Johnson Ryan Grant Jarius Wright Jason Avant Junior Hemingway De’Anthony Thomas Kevin Smith Frankie Hammond Adam Thielen Chandler Worthy Darrius Heyward-Bey Jamel Johnson Greg Little Keith Mumphery

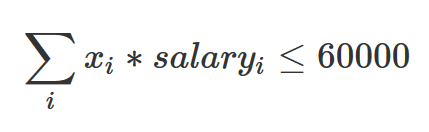
In this case, the direction of our first constraint is going to be less-than-or-equal-to (<=) and the value on the right-hand side will be 60,000. Again, the xis are implicit:

# Instantiate the vectors
f.dir <- rep(0, nrow(f.con))
f.rhs <- rep(0, nrow(f.con))

f.dir[1] <- "<="
f.rhs[1] <- 60000

Next, we are required to have 1 and only 1 defense. This requires an = for the direction of the constraint and a 1 for the rhs.

f.dir[2] <- "="
f.rhs[2] <- 1

For the other positions, we are required to have 1 K, 1 QB, at least 2 RB, at least 1 TE, at least 3 WR, and exactly 7 6 RB/TE/WR (to account for the _lack of a _flex).

f.dir[3:nrow(f.con)] <- c("=", "=", ">=", ">=", ">=", "=")
f.rhs[3:nrow(f.con)] <- c(1, 1, 2, 1, 3, 6)

For the full view of the coefficients, direction, and constraints similar to that in the helpfile, I’ll print out a data.frame:

kable(data.frame(f.con, f.dir, f.rhs), format = "markdown", row.names = T)

Seattle.Seahawks Kansas.City.Chiefs Houston.Texans Pittsburgh.Steelers Minnesota.Vikings Green.Bay.Packers Cincinnati.Bengals Washington.Redskins Steven.Hauschka Chris.Boswell Mike.Nugent Cairo.Santos Blair.Walsh Dustin.Hopkins Nick.Novak Mason.Crosby Russell.Wilson Ben.Roethlisberger Aaron.Rodgers Kirk.Cousins Andy.Dalton Alex.Smith Brian.Hoyer Teddy.Bridgewater AJ.McCarron Brandon.Weeden Landry.Jones Chase.Daniel Tarvaris.Jackson Shaun.Hill Robert.Griffin.III Keith.Wenning Colt.McCoy Scott.Tolzien Adrian.Peterson DeAngelo.Williams Marshawn.Lynch Jeremy.Hill Christine.Michael Charcandrick.West Eddie.Lacy James.Starks Fitzgerald.Toussaint Jordan.Todman Alfred.Blue Giovani.Bernard Jerick.McKinnon Alfred.Morris Matt.Jones Spencer.Ware Matt.Asiata Bryce.Brown Fred.Jackson Akeem.Hunt Chris.Thompson Chris.Polk Derrick.Coleman Knile.Davis Darrel.Young Isaiah.Pead John.Crockett Pierre.Thomas Dri.Archer John.Kuhn Rex.Burkhead Jonathan.Grimes Jordan.Reed Tyler.Eifert Travis.Kelce Heath.Miller Richard.Rodgers Kyle.Rudolph Luke.Willson Ryan.Griffin Tyler.Kroft Justin.Perillo C.J..Fiedorowicz MyCole.Pruitt C.J..Uzomah Garrett.Graham Demetrius.Harris Chase.Coffman Cooper.Helfet Brian.Parker Kennard.Backman Jesse.James Rhett.Ellison Antonio.Brown DeAndre.Hopkins A.J..Green Doug.Baldwin Jeremy.Maclin DeSean.Jackson Martavis.Bryant Randall.Cobb Pierre.Garcon Tyler.Lockett Jermaine.Kearse Markus.Wheaton Stefon.Diggs James.Jones Marvin.Jones Davante.Adams Nate.Washington Cecil.Shorts Mohamed.Sanu Jaelen.Strong Albert.Wilson Brandon.Tate Chris.Conley Mike.Wallace Jamison.Crowder Jeff.Janis Jared.Abbrederis Rashad.Ross Cordarrelle.Patterson Charles.Johnson Ryan.Grant Jarius.Wright Jason.Avant Junior.Hemingway De.Anthony.Thomas Kevin.Smith Frankie.Hammond Adam.Thielen Chandler.Worthy Darrius.Heyward.Bey Jamel.Johnson Greg.Little Keith.Mumphery f.dir f.rhs

opt <- lp("max", f.obj, f.con, f.dir, f.rhs, all.bin = TRUE)
picks <- fd[which(opt$solution == 1), ]
kable(picks, format = "markdown", row.names = F)

That’s the math that I used to not win at daily fantasy sports. Like I wrote, there are more tweaks that you could use to enhance it. I used some of them and ignored others, but it didn’t really work for me. The point is: The algorithm is broadly applicable and you should think about using it outside of fantasy football. If you want the code that generated the Algorithm part of the post, it’s available here and the data is here (the file extensions should be .rmd and .csv, but Wordpress is oddly picky about such things).

Go Blackhawks!

Correction: In the original version of this post I mistakenly added a flex position. AFAIK Fanduel doesn’t have a flex option, but my code does. I’ve since adjusted the code by decreasing the flex constraint from 7 to 6; i.e.

```f.rhs[3:nrow(f.con)] <- c(1, 1, 2, 1, 3, 6)`